Reinforcement learning

ME 343; March 13th, 2019

Prof. Eric Darve

YouTube will not let you play this video from this web site. Follow the link Watch this video on YouTube on the error page to see the video.

Recap on reinforcement learning

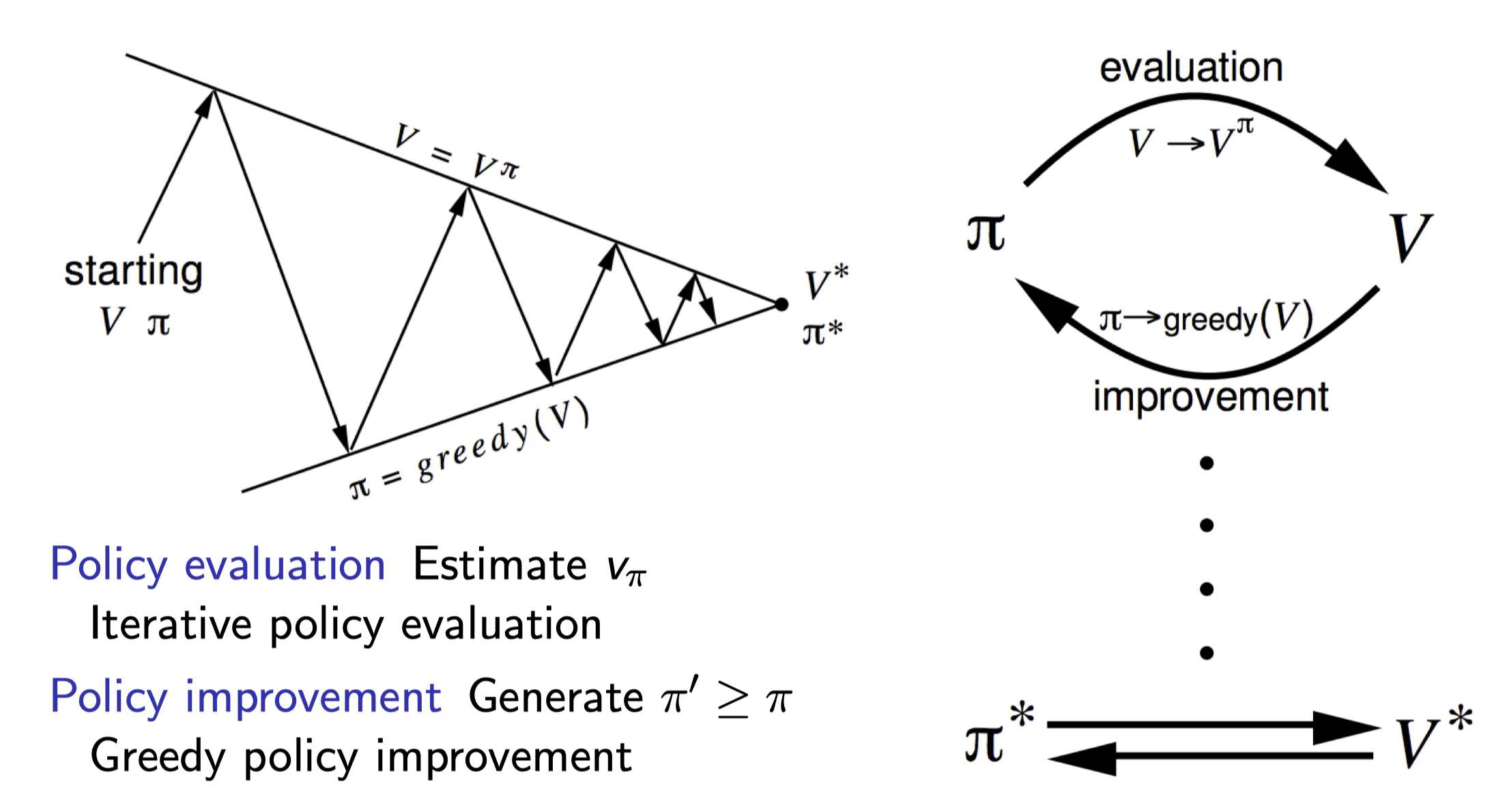
• Case 1: a model for the environment is known.

• Bellman equation can be used to calculate various quantities like the value function

$v(s) = E[R_t | S_t = s] + \gamma \sum_{s'} P_{ss'} v(s')$

Control! Optimal value function

Iterate:

• Policy evaluation: update value function based on policy
  $v_{k+1}(s) = \sum_{a} \pi_k(a|s) \Big( R^a_s + \gamma \sum_{s'} P^a_{ss'} \; v_k(s') \Big)$
• Policy improvement using greedy approach:
  $\text{argmax}_{a} \; \Big[ R^a_s + \gamma \sum_{s'} P^a_{ss'} v_{k+1}(s') \Big]$

Case 2: model-free learning

• For cases where the environment is too large to be completely evaluated or simply unknown
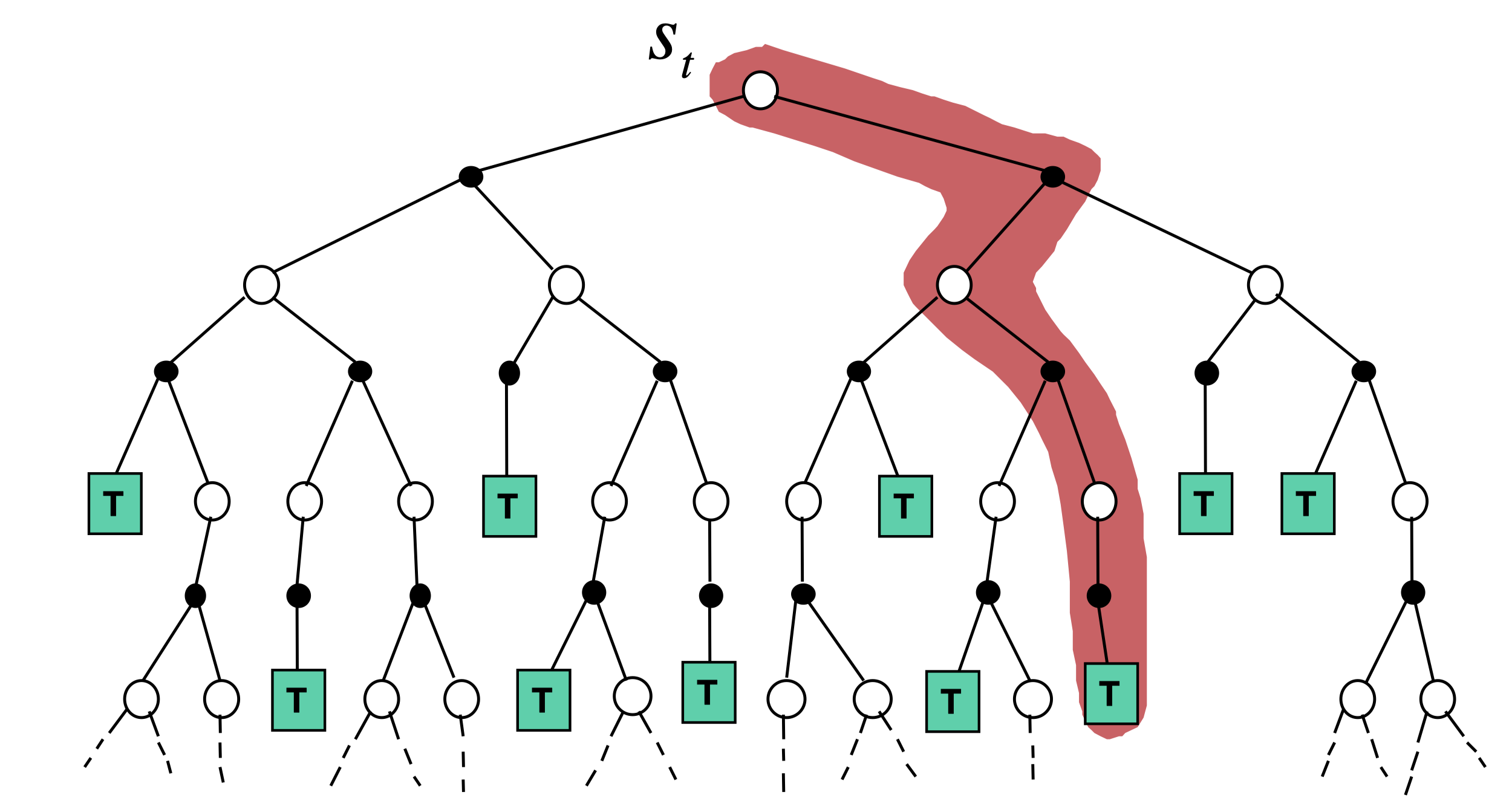
• Learn based on Monte-Carlo sampling

Full episodes

$V(S_t) \leftarrow V(S_t) + \alpha (G_t - V(S_t))$

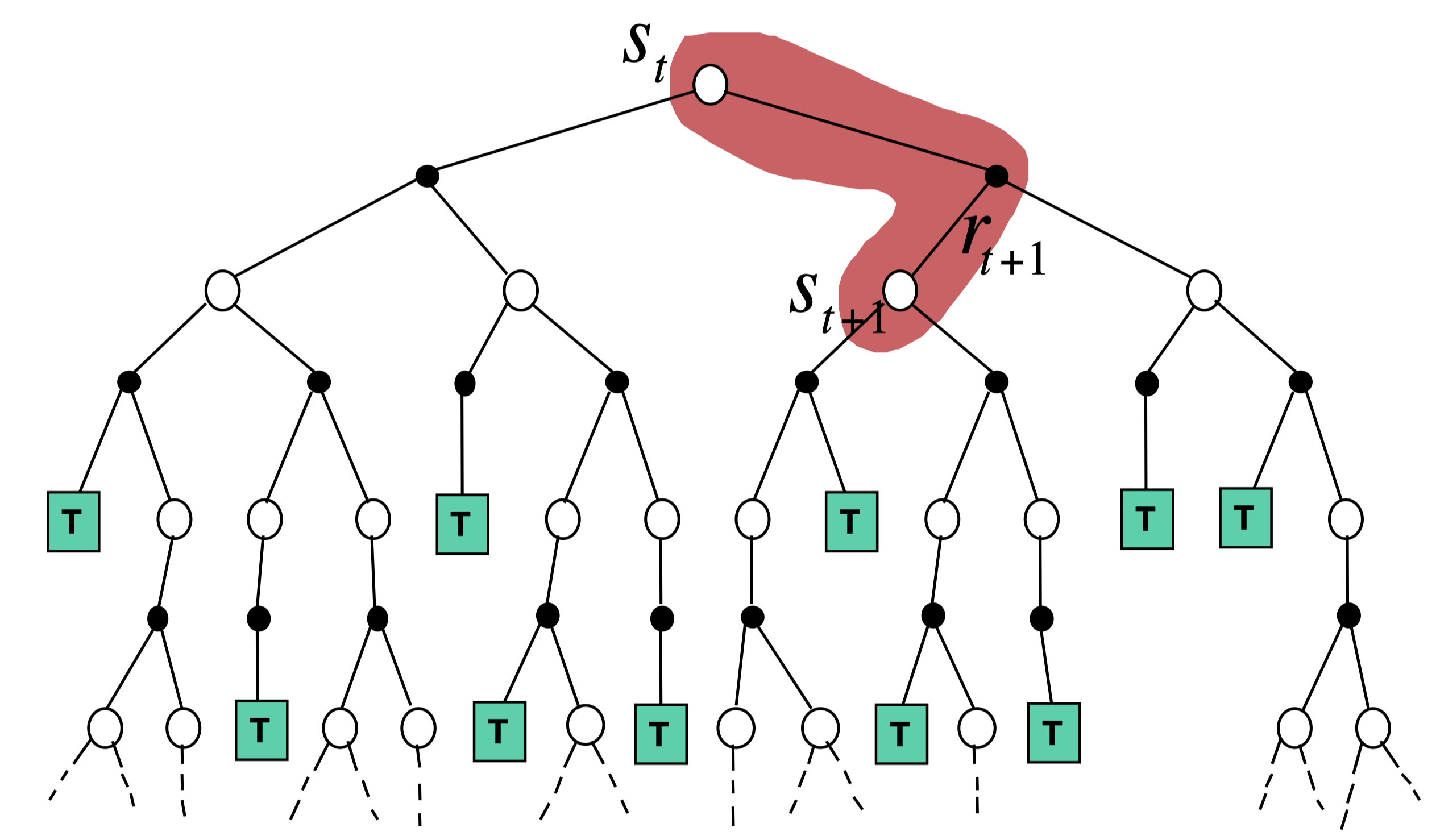
Temporal-difference backup

$V(S_t) \leftarrow V(S_t) + \alpha ( R_{t+1} + \gamma V(S_{t+1}) - V(S_t))$

Policy gradient

• Policy function may be approximated using a neural network
• This allows using gradient methods to improve the policy

$\pi(a|s,\theta) = P(A_t = a | S_t = s, \theta_t = \theta)$

$\theta$: parameterization of $\pi$.

• Example
  $\pi(a|s,\theta) = \frac{e^{\phi(s,a)^\top \theta}}{\sum_a e^{\phi(s,a)^\top \theta}}$
• $\phi(s,a)$: vector of features; $(\phi_1(s,a), \ldots, \phi_k(s,a))$.

Policy gradient theorem (see notes)

Gradient used to update weights $\theta$:
$\nabla_\theta J(\theta) \propto E_\pi \big[ G_t \; \nabla_\theta \ln \pi(A_t|S_t, \theta) \big]$

• $G_t$: discounted reward (MC sampling)
• $\pi(A_t|S_t, \theta)$: parameterized policy
• There is a coefficient of proportionality but this is not important for gradient algorithms

REINFORCE algorithm

Algorithm:

Repeat until convergence:
    Generate an episode S0, A0, R1,...,RT
    using policy pi(theta)
    For each step t of this episode:
        G <- return at step t
        Update theta using the eq. REINFORCE

$\theta \leftarrow \theta + \alpha \; \gamma^t \; G_t \; \nabla_\theta \ln \pi(A_t|S_t, \theta) \qquad \text{(REINFORCE)}$

AlphaGo!

• AlphaGo: computer program that defeated a Go world champion. Arguably the strongest Go player in history.
• Invented highly innovated Go moves.
• Let's play go!

Ingredients

Uses a combination of several of the methods we have seen:

• Neural network to approximate policy and value functions
• Monte-Carlo tree search with temporal difference
• Policy gradient theorem to improve policy
• UCT (multi-armed bandit) strategy to select moves

Neural networks: self-play

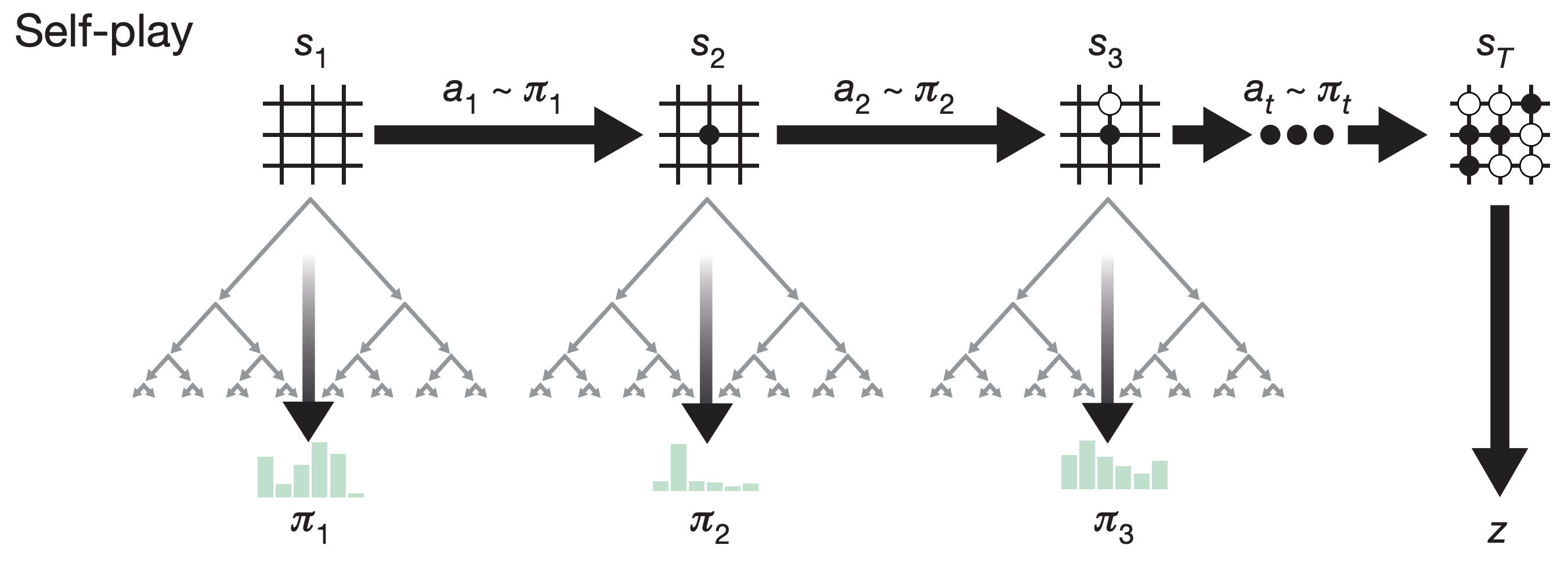
• Program plays a game $s_1$, $\dots$, $s_T$ against itself.
• An MCTS is executed using the latest neural network $f_\theta$.
• Moves are selected according to the search probabilities computed by the MCTS, $\pi_t$.

Neural networks: policy/value functions

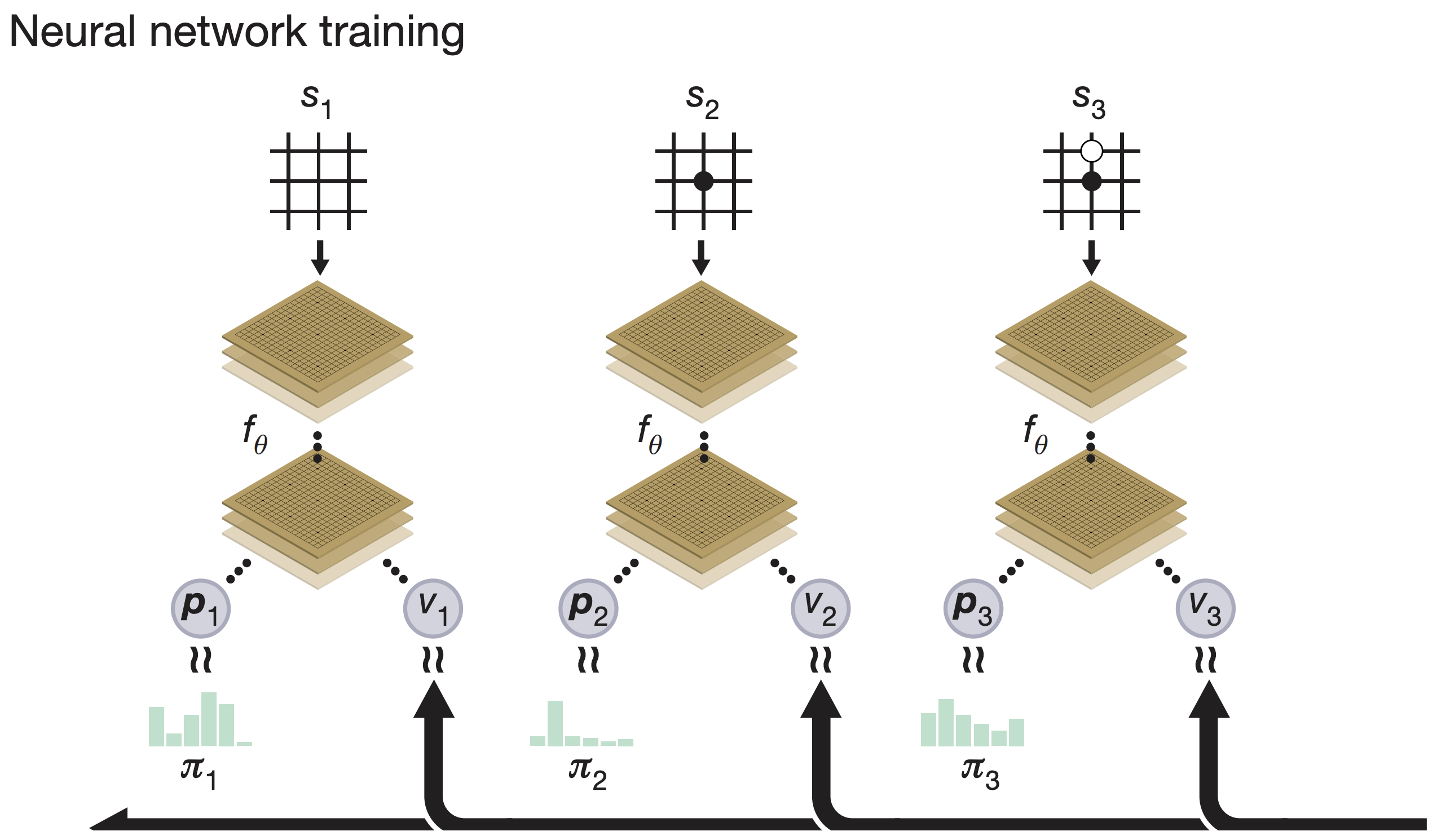
Neural networks: policy/value functions

Neural network parameters $\theta$ are updated to:

• maximize the similarity of the policy $p_t$ to the search probabilities $\pi_t$, and to
• minimize the error between the predicted winner $v_t$ and the game winner $z$.

Example of MCTS

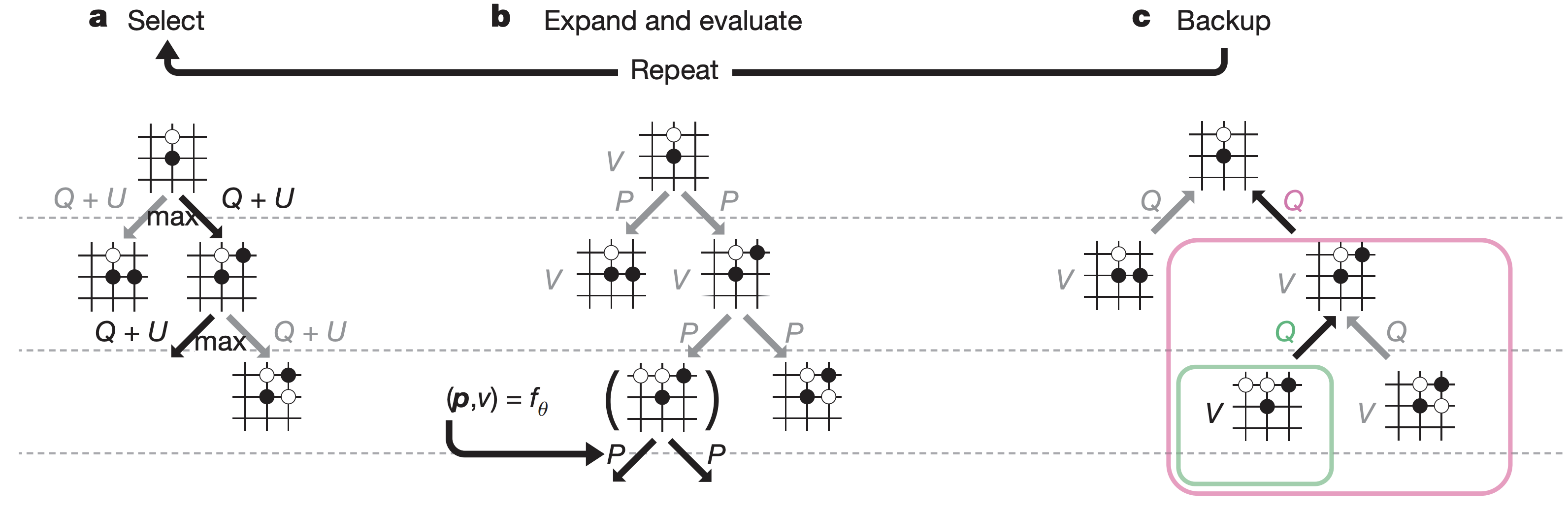
Policy improvement

Use the policy gradient theorem!

$\Delta \theta \propto z_t \nabla_\theta \ln \pi_\theta(A_t | S_t)$

UCT

Variant of PUCT algorithm was used:

$\begin{gathered} a_t = \text{argmax} \; Q(s_t, a) + U(s_t, a) \\ U(s,a) = C \; P(s,a) \; \frac{\sqrt{\sum_b N(s,b)}}{1 + N(s,a)} \end{gathered}$

• Added $P(s,a)$ to bias towards winning moves
• Abandoned log in favor of $\sqrt{}$. This leads to more exploration.

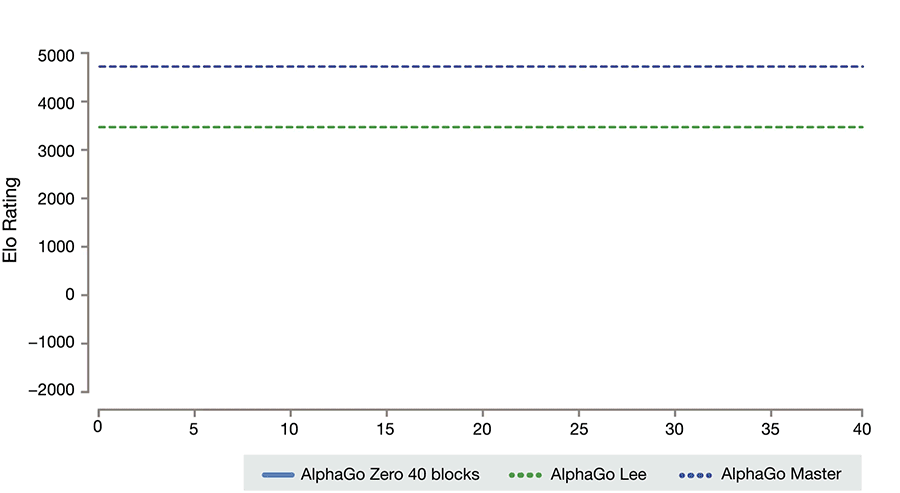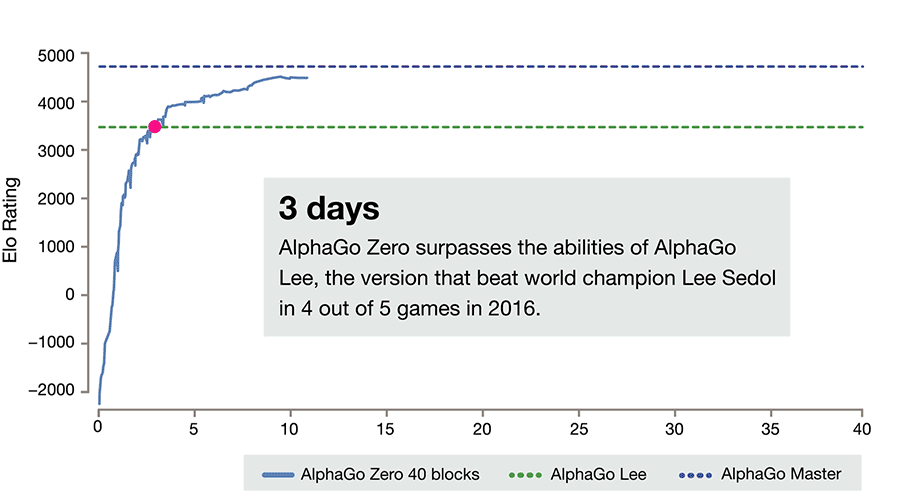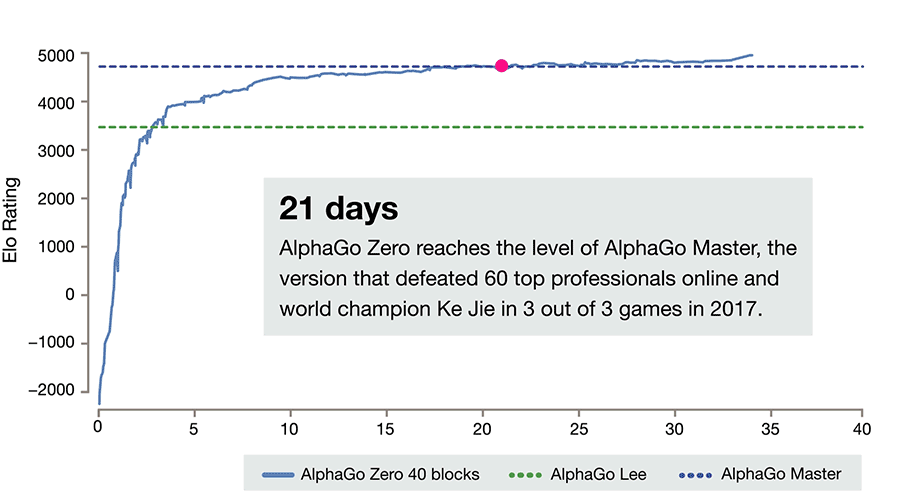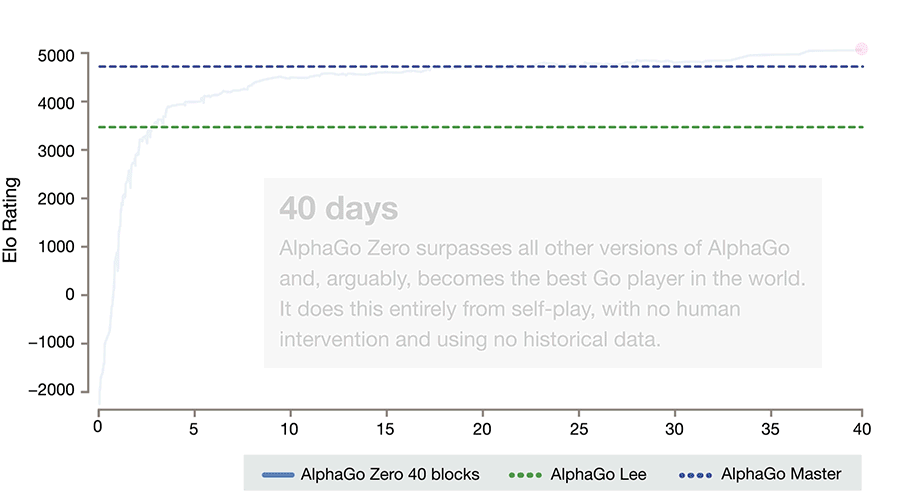
Training time graph

Joseki

• Joseki: corner sequences common in professional Go
• Noew slide: frequency of occurrence over time during training for different joseki
• Ultimately, AlphaGo preferred new joseki variants that were previously unknown!

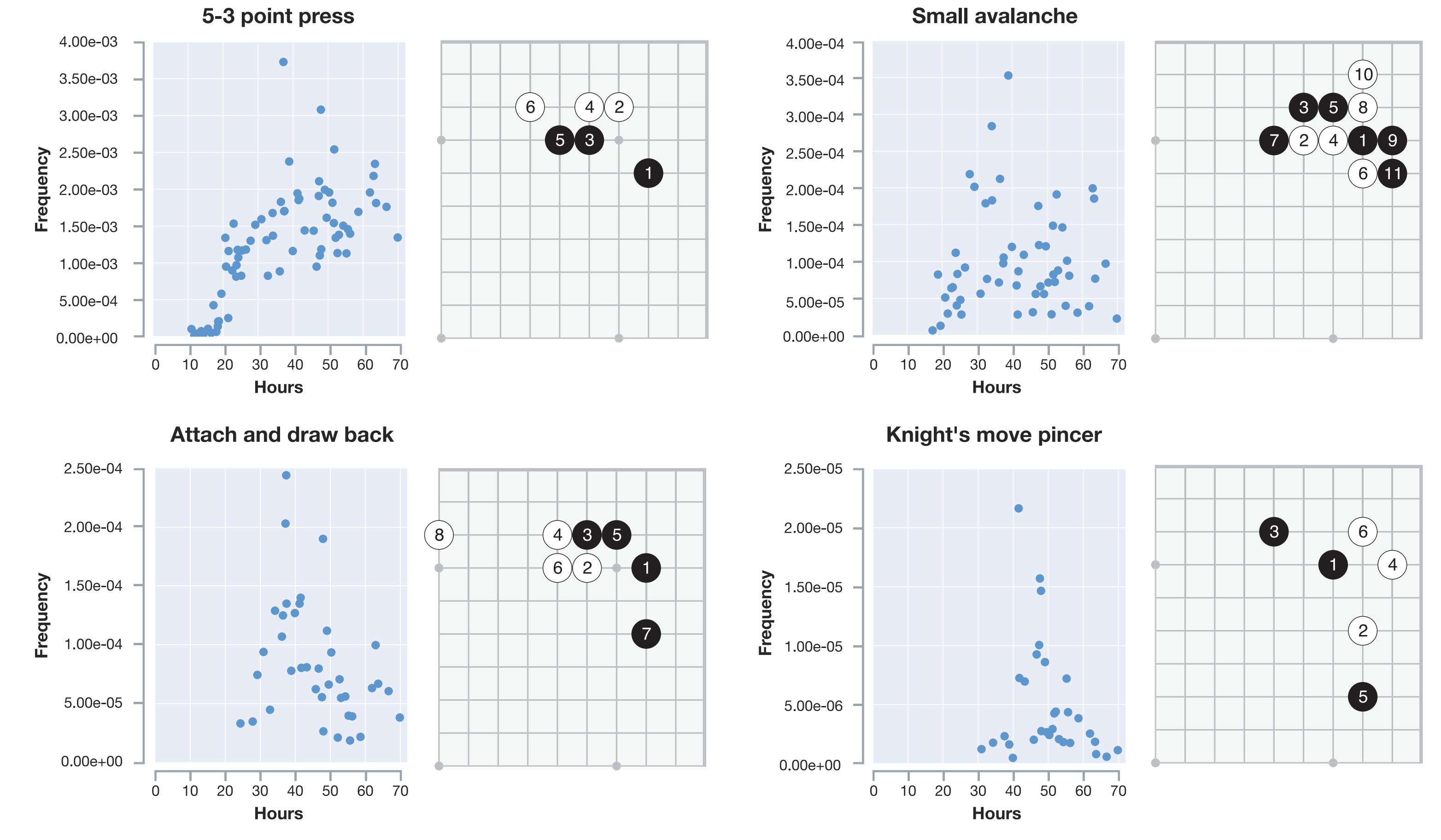
Training time is shown on the $x$-axis.

Strategies learned by AlphaGo

Try out AlphaGo

You pick select moves and see how the game evolves from there.

https://alphagoteach.deepmind.com/

GitHub codes

https://github.com/suragnair/alpha-zero-general

https://github.com/yhyu13/AlphaGOZero-python-tensorflow

https://github.com/leela-zero/leela-zero